Question

A circle in the xy-plane is centered at (3, 0) and has a radius with endpoint (1, 8 3 ). Which answer choice is an equation of the circle?

Answer 1

`(x-3)^2 + y^2 = 68`

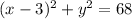
Explanation:

The vertex form of the equation of a circle is
`(x-h)^2 + (y-k)^2 = r^2` where (h,k) is the center of the circle and r is the radius. This circle has center (3,0). Find the radius using the distance formula with (3,0) and (1,8).

`d = √((x_2-x_1)^2 + (y_2-y_1)^2)  \\d = √((3-1)^2 + (0-8)^2)\\d = √((2)^2 + (-8)^2)  \\d = √(4 + 64)  =√(68)`

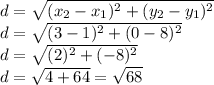
Substitute h = 3, k = 0 and r = √68 into the vertex form. Then simplify for the equation.

`(x-h)^2 + (y-k)^2 = r^2\\(x-3)^2 + (y-0)^2 = √(68)^2\\ (x-3)^2 + y^2 = 68`