Question

What is the additive inverse of 21i

Answer 1

The additive inverse of 21i is -21i

Explanation:

Let b be a real or complex number, the additive inverse of b is defined as a number x, such that:

`b + x = 0`

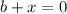
So, if we clear x from the equation, we get:

`x = -b`

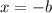
Then the additive inverse of a number b is -b. In other words, the additive inverse of a number is the one that when you add it to the previous number the result is 0.

In this case we have a complex number.

Then:

`b = 21i`.

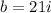Where
`i = √(-1)`

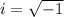
So

`21i + x = 0`

`x = -21i`.

The additive inverse of 21i is -21i