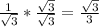Answer:
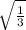
or
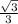
Explanation:
The expression
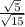 can be simplified by first writing the fraction under one single radical instead of two.
can be simplified by first writing the fraction under one single radical instead of two.
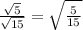
5/15 simplifies because both share the same factor 5.
It becomes
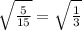
This can simplify further by breaking apart the radical.
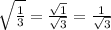
A radical cannot be left in the denominator, so rationalize it by multiplying by √3 to numerator and denominator.