Question

The scatterplot shows the ages and finishing times of seven men who ran a charity 5K run. Use the labeled points to create a linear model that predicts the race time (y) of a man of any age (x). Which equation represents this linear model?

y=o.47x+7.72
y=0.47x+29.15
y=2.146x-27.57
y=2.146x-2.07

Answer 1

A

Explanation:

E2020

Answer 2

0.47x + 7.72

Explanation:

We have to create a Linear model using the given two points on the graph. The two points are: (21, 17.5) and (43, 2.75)

The general equation of the line in slope intercept form is

y = mx + c

where m is the slope and c is the y-intercept.

Calculating the slope:

`slope=m=\frac{\textrm{Difference of y coordinates}}{\textrm{Difference of x coordinates}} \\\\ slope=m=(27.75-17.5)/(43-21)\\\\m=0.47`

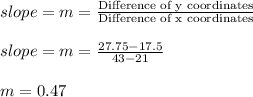
Using the value of m in above equation we get:

y = 0.47x + c

Calculating the y-intercept:

Using any of the given points we can calculate the value of c. Using the point (21, 17.5) in the above equation, we get:

17.5 = 0.47(21) + c

c = 17.5 - 0.47(21)

c = 7.63

Therefore, the equation is:

y = 0.47x + 7.63

Hence option a is the correct answer. The slight change in the value of "c" is because of rounding the value of m to 2 decimal places.

So from the given options, the correct answers is:

y = 0.47x + 7.72