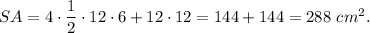Answer:
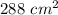
Explanation:
Consider the triangle AEB. This is isosceles triangle, because AE=EB. Thus, adjacent to the base AB angles are congruent, ∠EAB=∠EBA=45°. So, ∠AEB=180°-45°-45°=90°. We get the right isosceles triangle AEB, in which AE=6√2 cm. By the Pythagorean theorem,
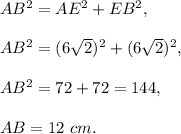
The height to the base of the isosceles triangle is the median, the median to the hypotenuse in right triangle is half of the hypotenuse, so the height is 6 cm. The surface area of the pyramid consists of 4 side's area and the area of the base square. Hence,