ANSWER
The first choice is correct.
Step-by-step explanation
We want to use the unit circle to determine the sine, cosine and tangent of the angle,
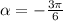
This simplifies to
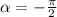
This is a quadrantal angle. This angle intercepts the unit circle at, (0,-1).
We know that on the unit circle, the x-coordinate is given by;

Hence

and the y-coordinate is given by;
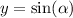
This implies that

The tangent is
![\tan( \alpha ) = ( \sin( \alpha ) )/( \cos( \alpha ) ) = ( - 1)/(0) = undefined]()
The correct choice is A.