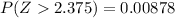Question

The probability that an appliance is in repair is 0.8. if an apartment complex has 100 such appliances, what is the probability that at least 90 will be in repair? use the normal approximation to the binomial.

Answer 1

`P(X\geq90) =0.00878`

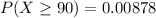
Explanation:

This situation can be modeled by a binomial distribution of parameters:

`p = 0.8\\\\q = 0.2\\\\n = 100`

We want to find the probability that at least 90 are in repair.

We can approximate this problem to a normal distribution, where:

`\mu = np`

`\mu = 80`

`\sigma = √(npq)\\\\\sigma = 4`

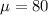
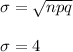
Then we look for

`P(X\geq90) = P(X>90 -0.5)\\\\P(X\geq90) = P(X>89.5)`

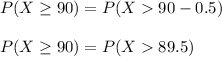
Then we must find the normal standard statistic Z-score

`Z = (X-\mu)/(\sigma)`

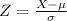
Therefore:

`P(X>89.5) = P((X-\mu)/(\sigma)>(89.5-80)/(4))\\\\P(X>89.5) =P(Z>2.375)`

Looking in the standard normal table we obtain:

`P(Z>2.375) = 0.00878`