For this case we must find the solutions of the following inequality:
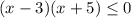
For
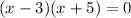 we have the following solutions:
we have the following solutions:
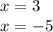
As a possible solution we have the following intervals:
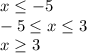
We must choose a value included in each of the possible intervals, replace them in the original inequality and verify if it is fulfilled.
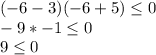
It is not true
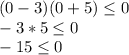
It is true.
ANswer:
Option C