Question

Let v1=(3,5) and v2=(-4,7).

(a) Compute |v1| and |v2|

(b) Compute the unit vectors in the direction of |v1| and |v2|.

(c) Draw and label v1, v2 and their unit vectors on the axes provided.

Answer 1

PART A

The given vectors are,


`v_1 = \: < \: 3 , \: 5 \: >`


`v_2 = \: < \: - 4 , \: 7 \: >`

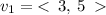
The magnitude of the vector


`v= \: < \: x , \: y \: > \:`

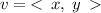
is given by:


`|v| = \sqrt{ {x}^(2) + {y}^(2) }`

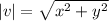
This implies that,


`|v_1| = \sqrt{ {3}^(2) + {5}^(2) }`


`|v_1| = √(9 + 25)`


`|v_1| = √(34)`


`|v_2| = \sqrt{ {( - 4)}^(2) + {7}^(2) }`


`|v_2| = √( 16+ 49)`


`|v_2| = √(65)`

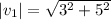
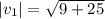
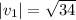
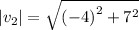
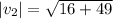
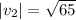
PART B

To find the unit vector in the direction of a given vector, we divide by the magnitude of that vector.


`^( - ) _(v_1) = \: < \: (3)/( √(34) ) , \: (5)/( √(34) ) \: >`

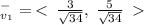
Rationalize the denominator.


`^( - ) _(v_1) = \: < \: (3√(34))/( 34 ) , \: (5√(34))/( 34 ) \: >`

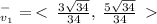
Also,


`^( - ) _(v_2) = \: < \: ( - 4)/( √(65) ) , \: (7)/( √(65) ) \: >`


`^( - ) _(v_2) = \: < \: ( - 4√(65))/( 65 ) , \: (7√(65))/( 65 ) \: >`

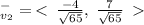
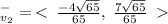
PART C

The sketch of the given vectors as well as their unit vectors are shown in the attachment.