Question

What us the value of the discriminant of the quadratic equation -2^2=-8x+8 and what does its value mean about the number of a real number solutions the equation has

Answer 1

The discriminant is zero.

The given equation has one real root.

Step-by-step explanation

The given quadratic equation is:

`- 2 {x}^(2) = - 8x + 8`

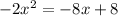
We rewrite this in the form;

`a {x}^(2) + bx + c = 0`

`- 2 {x}^(2) + 8x - 8 = 0`

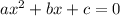
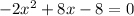
This means that,

a=-2, b= 8, c=-8

The discriminant is given by;

D=b² - 4ac

That is:

`D = {8}^(2) - 4( - 2)( - 8)`

`D = 64 - 64 = 0`

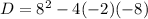
Therefore the discriminant is zero.

This tells us that the quadratic equation has one real root.

In order words, the given quadratic equation has a repeated real root.