ANSWER
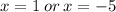
EXPLANATION
The given rational expression is
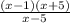
For the given rational function to be zero, then the numerator must be equal to zero.
We now equate the numerator to zero and solve for x.
This implies that,
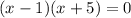
We use the zero product property to obtain,
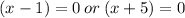
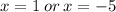
Hence the zeros of the given rational function are x=-5,x=1