Answer:
Option a. (-5, 2)
Explanation:
The focus of a parabola is a point. Regarding this point, each point of the parabola has the same distance to a line that is known as "directrix".
By definition, for a parabola of the form:

The focus of the parable is given by the point: (h, k +p)
We must identify the values of h, k and p for the given equation.
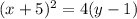
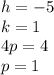
Now that we know the values of h, k and p we can find the focus
The focus is
(-5, 1+1)
(-5, 2).