Which point is NOT part of the solution of the inequality y ≥ −|x − 4| − 3? (–1, 1) (4, –4) (–3, 2) (0, 0)

Question

asked Feb 4, 2020 196k views

1 Answer

TarJae · Answer 1 · 2020-02-08T09:53:25+0000

ANSWER

(4,-4)

Step-by-step explanation

The given inequality is

$y \geqslant - |x - 4| - 3$

If (-1,1) satisfies this inequality, then it is a solution.

We substitute x=-1 and y=1 into the inequality to get,

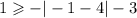
$1 \geqslant - | - 1 - 4| - 3$

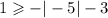
$1 \geqslant - | -5| - 3$

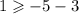
$1 \geqslant - 5- 3$

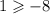
$1 \geqslant - 8$

This is true. Hence (-1,1) is a solution.

We check for (4,-4) also.

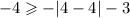
$- 4 \geqslant - |4- 4| - 3$

$- 4 \geqslant 0 - 3$

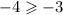
$- 4 \geqslant- 3$

This is false. Hence (4,-4) is not a solution.

Checking for (-3,2).

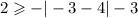
$2 \geqslant - | - 3- 4| - 3$

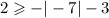
$2 \geqslant - | -7| - 3$

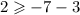
$2 \geqslant - 7 - 3$

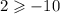
$2 \geqslant - 10$

This is true. Hence (-3,2) is a solution to the inequality.

Checking for (0,0)

$0 \geqslant - |0- 4| - 3$

$0 \geqslant - 4 - 3$

$0 \geqslant - 7$

This is true. Hence (0,0) is also a solution.

The correct choice is (4,-4)