Hello!
The answer is:
The expression that represents the width of the rectangle is:
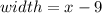
Why?
We know that the area of a rectangle is equal to:
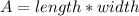
We are given the function that represents the area of the rectangle and one of its sides, the length is equal to (x+8)
So, rewriting we have:
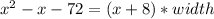
The coefficients of the variables of the given function are:
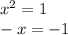
Now, to find the width, we need to find two numbers which its product gives as result "-72" and its addition gives as result the coefficient of the linear term of the function (x), its "-1".
Then,
We know that,
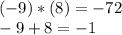
So, the factors of the given function are:
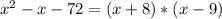
Since, we already know that the length corresponds to "x+8", we know that the width corresponds to "x-9".
Proving that the factors are right,
Applying the distributive property, we have:
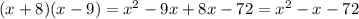
Hence, the equation is satisfied and we can conclude that:
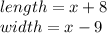
Have a nice day!