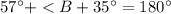Question

(This is a "show your work" type of assignment)

1. Can you use Pythagorean Theorem to find the missing side? Why or why not?

2. Would you use Law of Sine or Law of Cosine to find the length of side CB? Explain your answer.

3. Find the length of side CB. Show your work and round your answer to the nearest whole number.


4. Find the measure of angle C. (Hint: use the other “Law”). Round your answer to the nearest whole degree.


5. What is the measure of angle B? Show your work and round your answer to the nearest whole degree.

Answer 1

Part 1) It is not possible to apply the Pythagorean Theorem to find the missing side, because is not a right triangle

Part 2) I would use the law of the cosine, because to apply the law of sine I would need to know the value of angle C or angle B

Part 3) The length of side CB is
`369\ units`

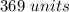
Part 4) The measure of angle C is
`35\°`

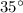
Part 5) The measure of angle B is
`88\°`

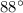
Explanation:

Part 1) Can you use Pythagorean Theorem to find the missing side?

we know that

The Pythagorean Theorem is used in a right triangle

The triangle ABC of the figure is not a right triangle

therefore

It is not possible to apply the Pythagorean Theorem to find the missing side

Part 2) Would you use Law of Sine or Law of Cosine to find the length of side CB?

I would use the law of the cosine, because to apply the law of sine I would need to know the value of angle C or angle B

Part 3) Find the length of side CB. Show your work and round your answer to the nearest whole number

Applying the law of cosine

`BC^(2)=AB^(2)+AC^(2)-2(AB)(AC)cos(A)`

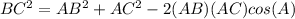
substitute the values

`BC^(2)=255^(2)+440^(2)-2(255)(440)cos(57\°)`

`BC^(2)=136,408`

`BC=369\ units`

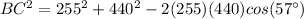
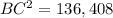
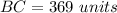
Part 4) Find the measure of angle C. (Hint: use the other “Law”). Round your answer to the nearest whole degree

Applying the law of sines

`(AB)/(sin(C))=(CB)/(sin(A))`

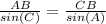
substitute the values

`(255)/(sin(C))=(369)/(sin(57\°))`

`sin(C)=255*sin(57\°)/369=0.5796`

`C=arcsin(0.5796)=35\°`

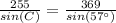
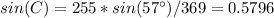
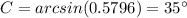
Part 5) What is the measure of angle B? Show your work and round your answer to the nearest whole degree.

Remember that

the sum of the interior angles of a triangle must be equal to 180 degrees

sp

`<A+<B+<C=180\°`

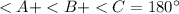
substitute the values and solve for <B

`57\°+<B+35\°=180\°`

`<B=180\°-92\°=88\°`