Question

How is the graph of y -3x2 +2 different from the graph of y - 3x2?

Answer 1

Difference between graphs of both equation is the vertex of the both curves.

Explanation:

Given Equations of curves are
`y=-3x^2+2\:\:and\:\:y=-3x^2`

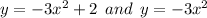
We need to find the difference in the graphs of the given curves.

one variable in both curves has degree 2 and 2nd variable in both curves has degree 1.

So, Given Equation of curves are of parabola.

Consider 1st equation,

y = -3x² + 2

`x^2=(-1)/(3)(y-2)`

Vertex of this parabola is ( 0 , 2 )

Axis of symmetry is y-axis.

Consider 2nd equation,

y = -3x²

`x^2=(-1)/(3)y`

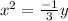
Vertex of this parabola is ( 0 , 0 )

Axis of symmetry is y-axis.

Therefore, Difference between graphs of both equation is the vertex of the both curves.

Figures are attached.