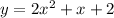Question

A parabola passes through the points (-2,8), (0,2), and (1,5). What function does the graph represent?

Answer 1

`y = 2 {x}^(2) + x + 2`

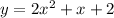
Step-by-step explanation

Let the function that represent the graph be:

`y = a {x}^(2) + bx + c`

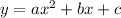
The parabola passes through the points (-2,8), (0,2), and (1,5).

These points must satisfy the function.

For (-2,8), we have

`8= a{( - 2)}^(2) + b( - 2) + c`

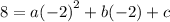
This implies that that,

`4a - 2b + c = 8...(1)`

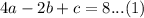
For (0,2), we have,

`2= a{( 0)}^(2) + b( 0) + c`

This implies that,

`c = 2`

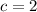
For (1,5), we have

`5= a{( 1)}^(2) + b( 1) + c`

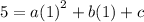
This implies that,

`a + b + c = 5...(2)`

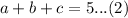
Put c=2 into equation (1) and (2).

`4a - 2b + 2 = 8`

`4a - 2b = 8 - 2`

`4a - 2b = 6`

`2a - b = 3...(3)`

`a + b + 2=5`

`a + b =5 - 2`

`a + b = 3...(4)`

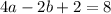
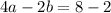
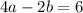
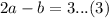
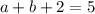
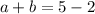
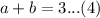
Add equation (3) and equation (4)

`3a = 6`

`a = 2`

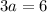
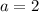
Put a=2 into equation (4).

`2 + b = 3`

`b = 3 - 2 = 1`

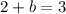
Therefore the function is

`y = 2 {x}^(2) + x + 2`