Question

Sophia and Tyler are running around a 400-meter track. They start running from the same place, at the same time. Sophia runs at a speed of 5 m/s and Tyler runs at a speed of 4 m/s. How long will it take Sophia to lap Tyler?

HELP FASTLY!
PLEASEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEE!

Answer 1

Hello!

The answer is: There will take 400 seconds to Sophia to lap Tyler.

Why?

To solve this problem we need to write equations in function to Tyler's distance when Sophia laps him, so:

Let be "x" the position of Tyler when Sophia is 400 m ahead of him.

Let be "x+400" the position of Sophia when she laps Tyler

Also, we must remember that time is equal to:

`t=(Distance)/(V)`

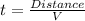
So, the equation to calculate the position of the Tyler when Shopia laps him, can be written like this:

`(Tyler'sDistance)/(Tyler'sSpeed)=(Tyler'sDistance+400)/(Sophia'sSpeed)`

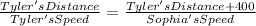
Then,

`(x)/(4(m)/(s) )=(x+400m)/(5(m)/(s))\\\\(5(m)/(s))*(x)=(4(m)/(s))(x+400m)\\\\(5(m)/(s))*(x)=(4(m)/(s))*(x)+(4(m)/(s))*400m\\\\(5(m)/(s))*(x)-(4(m)/(s))*(x)=1600(m^(2) )/(s)\\\\(1(m)/(s))*(x)=1600(m^(2) )/(s)\\\\x=(1600(m^(2) )/(s))*(s)/(m)=1600m`

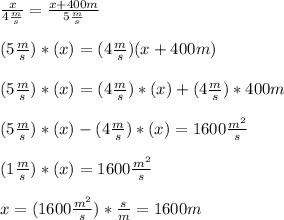
Therefore, the distance that Tyler's ridden when Sophia laps him is 1600m.

Let's calculate the time with the following formula:

`Tyler'sDistance=x=xo+v*t\\\\1600m=0+4(m)/(s)*t\\\\t=(1600m)/(4(m)/(s) )=400s`

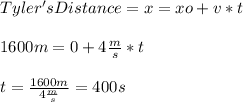
If we want to prove that the result is ok, let's substitutite the same distance in the Sophia's distance equation:

`x+400m=xo+v*t\\\\1600m+400m=0+5(m)/(s) *t\\2000m=5(m)/(s) *t\\\\5(m)/(s) *t=2000m\\\\t=(2000m)/(5(m)/(s) )=400s`

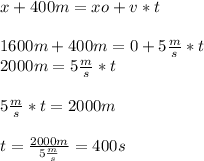
Hence,

There will take 400 seconds to Sophia to lap Tyler.

Have a nice day!