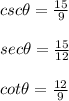Question

Determine the three reciprocal trigonometric ratios of the angle.

Answer 1

The correct option is:

Option: c and option: d

Explanation:

We know that with respect to the angle θ, the trigonometric ratios are defined as follows:

`\sin \theta=(opposite)/(Hypotenuse)\\\\\\\cos \theta=(adjacent)/(Hypotenuse)\\\\\\\tan \theta=(opposite)/(adjacent)\\\\\\\csc \theta=(Hypotenuse)/(opposite)\\\\\\\sec \theta=(hypotenuse)/(adjacent)\\\\\\\cot \theta=(adjacent)/(opposite)`

Now, we know that the side which is opposite to angle θ is of length: 9

The side which is adjacent to angle θ is of length: 12

and the hypotenuse of the triangle is: 15

Hence, we have:

`\sin \theta=(9)/(15)\\\\\\\cos \theta=(12)/(15)\\\\\\\tan \theta=(9)/(12)\\\\\\\csc \theta=(15)/(9)\\\\\\\sec \theta=(15)/(12)\\\\\\\cot \theta=(12)/(9)`

Answer 2

Answer: Option b.

Explanation:

The reciprocal trigonometric ratios are:

1) Cosecant (
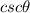`csc\theta`), which is the reciprocal of the sine.

2) Secant (
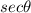`sec\theta`), which is the reciprocal of the cosine.

3) Cotangent (
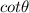`cot\theta`), which is the reciprocal of the tangent.

If:

`sin\theta=(opposite)/(hypotenuse)}\\\\cos\theta=(adjacent)/(hypotenuse)\\\\tan\theta=(opposite)/(adjacent)`

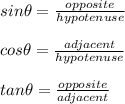
Then:

`csc\theta=(hypotenuse)/(opposite)}\\\\sec\theta=(hypotenuse)/(adjacent)\\\\cot\theta=(adjacent)/(opposite)`

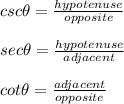
Knowing that:

`opposite=9\\adjacent=12\\hypotenuse=15`

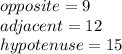
You can substitute these values into the trigonometric ratios to find the values of the reciprocal ratios of the angle
`\theta`:

`csc\theta=(15)/(9)}\\\\sec\theta=(15)/(12)\\\\cot\theta=(12)/(9)`