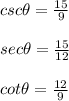Answer: Option b.
Explanation:
The reciprocal trigonometric ratios are:
1) Cosecant (
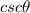 ), which is the reciprocal of the sine.
), which is the reciprocal of the sine.
2) Secant (
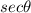 ), which is the reciprocal of the cosine.
), which is the reciprocal of the cosine.
3) Cotangent (
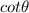 ), which is the reciprocal of the tangent.
), which is the reciprocal of the tangent.
If:
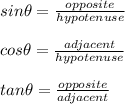
Then:

Knowing that:
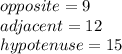
You can substitute these values into the trigonometric ratios to find the values of the reciprocal ratios of the angle
 :
: