Final answer:
The quadratic equation
 -6x-5=0 is solved using the quadratic formula to find its solutions, giving the answers x = 3 +
-6x-5=0 is solved using the quadratic formula to find its solutions, giving the answers x = 3 +
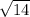 and x = 3 -
and x = 3 -
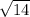 .
.
Step-by-step explanation:
To solve the quadratic equation
 -6x-5=0 using the quadratic formula, we first identify the coefficients a, b, and c from the general form a
-6x-5=0 using the quadratic formula, we first identify the coefficients a, b, and c from the general form a
 +bx+c=0. In this case, a=1, b=-6, and c=-5. The quadratic formula is:
+bx+c=0. In this case, a=1, b=-6, and c=-5. The quadratic formula is:
x = (-b ±
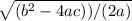
Plugging these values into the formula gives us:
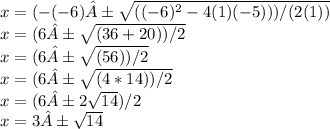
Therefore, the solutions for the quadratic equation are x = 3 +
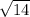 and x = 3 -
and x = 3 -
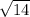 .
.