For this case we have that, by definition, two equivalent fractions are those that represent the same amount. In addition, two fractions are equivalent if the products of the numerator of one and the denominator of the other are equal, that is, cross products.
Example:
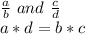
So, a fraction equivalent to

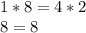
To obtain
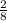 we must multiply:
we must multiply:
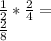
Answer:
