Question

30 POINTS AVAILABLE

1.
Write the equation of a circle with the endpoints of the diameter at (-1, 6) and (5, -4). Watch the signs!

Answer 1

`\large\boxed{(x-2)^2+(y-1)^2=34}`

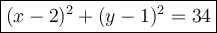
Explanation:

The equation of a circle in standard form:

`(x-h)^2+(y-k)^2=r^2`

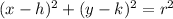
(h, k) - center

r - radius

We have the endpoints of the diameter: (-1, 6) and (5, -4).

Midpoint of diameter is a center of a circle.

The formula of a midpoint:

`\left((x_1+x_2)/(2);\ (y_1+y_2)/(2)\right)`

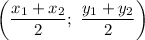
Substitute:

`h=(-1+5)/(2)=(4)/(2)=2\\\\k=(6+(-4))/(2)=(2)/(2)=1`

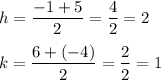
The center is in (2, 1).

The radius length is equal to the distance between the center of the circle and the endpoint of the diameter.

The formula of a distance between two points:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

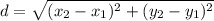
Substitute the coordinates of the points (2, 1) and (5, -4):

`r=√((5-2)^2+(-4-1)^2)=√(3^2+(-5)^2)=√(9+25)=√(34)`

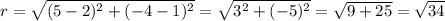
Finally we have:

`(x-2)^2+(y-1)^2=(√(34))^2`