Answer:
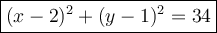
Explanation:
The equation of a circle in standard form:

(h, k) - center
r - radius
We have the endpoints of the diameter: (-1, 6) and (5, -4).
Midpoint of diameter is a center of a circle.
The formula of a midpoint:
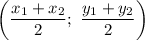
Substitute:
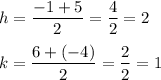
The center is in (2, 1).
The radius length is equal to the distance between the center of the circle and the endpoint of the diameter.
The formula of a distance between two points:

Substitute the coordinates of the points (2, 1) and (5, -4):
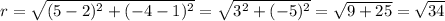
Finally we have:
