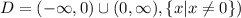Answer:
Domain of the function is
Explanation:
Given : Function f as a function of x is equal to four divided by x squared.
To find : Determine the domain of the function ?
Solution :
Writing function in numeral form,
f as a function of x is equal to four divided by x squared i.e.
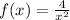
The domain of the function is all the x values for which f(x) is defined.
i.e. function is defined when denominator is not equal to zero.
So, We put denominator = 0 to get on which value of x function is not defined.
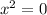

Therefore, Domain of the function is