Answer:
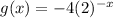
Explanation:
Given: The graph of f(x) (blue color)
f(x) reflection across x-axis to get g(x).
Using to find the equation of f(x)
The graph looks like a exponential decay whose y-intercept (0,4) and passing point (1,2).
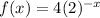
Reflection across x-axis
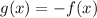
The function g(x) represents by
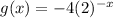
Hence, The
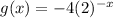 is reflection of f(x) across x-axis.
is reflection of f(x) across x-axis.