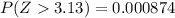Question

A set of normally distributed data has a mean of 3.2 and a standard deviation of 0.7. Find the probability of randomly selecting 30 values and getting a mean greater than 3.6.

Answer 1

Answer: 0.0009

Just took the test

Answer 2

`P(Z> 3.13) = 0.000874`

Explanation:

A set of normally distributed data has a mean of 3.2 and a standard deviation of 0.7. Find the probability of randomly selecting 30 values and obtaining an average greater than 3.6.

We can denote the population mean with the symbol
`\mu`

According to the information given, the data have a population mean:

`\mu = 3.2`.

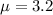The standard deviation of the data is:

`\sigma = 0.7`.

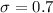Then, from the data, a sample of size
`n = 30` is taken.

We want to obtain the probability that the sample mean is greater than 3.6

If we call

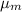`\mu_m` to the sample mean then, we seek to find:

`P(\mu_m> 3.6)`

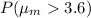
To find this probability we find the Z statistic.

`Z = (\mu_m-\mu)/(\sigma_(\mu_m))`

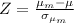
Where:

Where
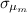`\sigma_(\mu_m)` is the standard deviation of the sample

`\sigma_(\mu_m) = (\sigma)/(√(n))`

`\sigma_(\mu_m) =(0.7)/(√(30))\\\\\sigma_(\mu_m) = 0.1278`

`P((\mu_m-\mu)/(\sigma_(\mu_m))> (3.6-3.2)/(0.1278))`

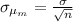
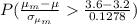
Then:

`Z = (3.6-3.2)/(0.1278)\\\\Z = 3.13`

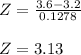
The probability sought is:
`P(Z> 3.13)`

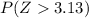
When looking in the standard normal probability tables for right tail we obtain:

`P(Z> 3.13) = 0.000874`