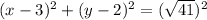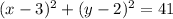Answer:
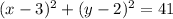
Explanation:
step 1
Find the diameter of the circle
the formula to calculate the distance between two points is equal to

we have
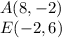
substitute the values
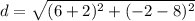
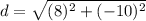
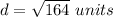
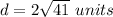
step 2
Find the center of the circle
The center is the midpoint of the diameter
The center is equal to
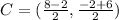
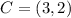
step 3
Find the equation of the circle
The equation of the circle in center radius form is equal to

we have
(h,k)=(3,2)
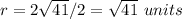 ---> the radius is half the diameter
---> the radius is half the diameter
substitute