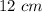Question

The shorter leg of a right triangle is 7 centimeters nbspless than the other leg. Find the length of the two legs if the hypotenuse is 13 centimeter

Answer 1

The shorter leg of the right triangle is
`5\ cm`

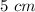
The other leg of the right triangle is
`12\ cm`

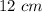
Explanation:

Let

x-----> the shorter leg of a right triangle

y----> the larger leg of a right triangle

we know that

Applying the Pythagoras Theorem

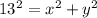`13^(2)=x^(2) +y^(2)` ----> equation A

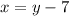`x=y-7` ----> equation B

substitute equation B in equation A and solve for y

`13^(2)=(y-7)^(2) +y^(2)\\169=y^(2) -14y+49+y^(2) \\2y^(2)-14y-120=0`

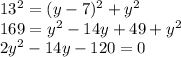
using a graphing tool----> solve the quadratic equation

The solution is
`y=12\ cm`

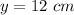
see the attached figure

Find the value of x

`x=12-7=5\ cm`

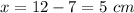
therefore

The shorter leg of the right triangle is
`5\ cm`

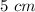
The other leg of the right triangle is
`12\ cm`