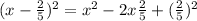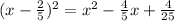Question

Expand the binomial

`(x-(2)/(5))^(2)`

Answer 1

`(x- (2)/(5))^(2) = x^2 -(4)/(5)x + (4)/(25)`

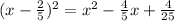
Explanation:

You have two methods to expand this binomial.

Method 1

If you have the expression:

`(x- (2)/(5))^(2)`

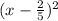
You can write the expression it in the following way:

`(x-(2)/(5))^(2)=(x-(2)/(5))(x-(2)/(5))`

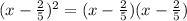
Then, apply the distributive property:

`(x-(2)/(5))(x-(2)/(5)) = x^2 -(2)/(5)x -(2)/(5)x+ ((2)/(5))(2)/(5)`

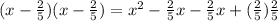
Simplify the expression:

`(x-(2)/(5))^2= x^2 -(4)/(5)x+ ((4)/(25))`

---------------------------------------------------------------------------------------

Method 2

For any expression of the form:

`(a-b)^2`

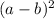
Its expanded form will be:

`(a-b)^2= a^2 -2ab + b^2`

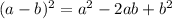
If

`a = x`

`b =(2)/(5)`

`(x- (2)/(5))^(2) = x^2 - 2x(2)/(5) + ((2)/(5))^2`

`(x- (2)/(5))^(2) = x^2 -(4)/(5)x + (4)/(25)`