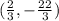Answer:
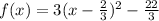
The vertex is
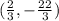
Explanation:
For a general quadratic function the form is:

For the function
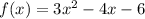
Take common factor 3.

The values of the coefficients for the function within the parenthesis are the following:
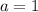 ,
,
 ,
,

Take the value of b and divide it by 2. Then, the result obtained squares it.
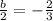
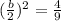
Add and subtract
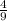
![f(x) = 3([x ^ 2 -(4)/(3)x +(4)/(9)]- 2-(4)/(9))](https://img.qammunity.org/2020/formulas/mathematics/high-school/v43yx2f2q3vjqxd5uzpf0zu8xi7q9xo2wg.png)
Write the expression of the form
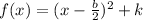
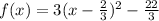
The vertex is