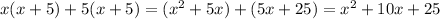Question

Expand the binomial

`(x+5)^(2)`

Answer 1

`x^(2) + 10x + 25`

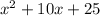
Explanation:

Let's first re-write the problem expression.

`(x +5)^(2)  = (x+5) (x+5)`

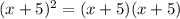
Then we apply the distributive property to get

(x + 5)(x+5) = x(x+5) + 5(x+5)

We broke up the first (x+5) to use the x and the 5 to multiply the second (x+5) element... then add them to each other (because of the + sign).

`x(x+5) + 5(x+5)  = (x^(2) + 5x) + (5x + 25) = x^(2) + 10x + 25`