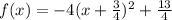Question

Transform the given quadratic function into vertex form f(x) = quadratic function into vertex form f(x) = quadratic function into vertex form
`f(x) = (x-h)^(2) + k` by completing the square.
`a(x-h)^(2) +k` by completing the square.


`f(x) = -4x^(2) -6x+1`

Answer 1

Answer:
`f(x)=-4(x+(3)/(4))^2+(13)/(4)`

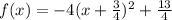
Explanation:

The Vertex form of a quadratic function is
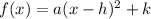`f(x)=a(x-h)^2+k`, where
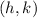`(h,k)` is the vertex of the parabola, and the sign of the coefficient
`a` indicates if the parabola opens down or opens up.

The Standard form of a quadratic function is
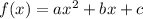`f(x)=ax^2+bx+c`, where the sign of the coefficient
`a` indicates if the parabola opens down or opens up.

To transform a quadratic function from Standard form to Vertex form, you need to complete the square.

Given the quadratic function
`f(x)=-4x^(2)-6x+1`:

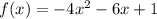Indentify a:

`a=-4`

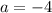
Factor out -4:

`f(x)=-4(x^2+(3)/(2)+(1)/(4))`

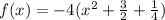
Take the coefficient b and add and subtract
`((b)/(2))^2` to keep the balance:

`((b)/(2))^2=(((3)/(2))/(2))^2=((3)/(4))^2`

`f(x)=-4(x^2+(3)/(2)x+((3)/(4))^2)-(1)/(4)-((3)/(4))^2)`

`f(x)=-4(x^2+(3)/(2)x+((3)/(4))^2)) +1+((9)/(4))`

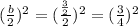
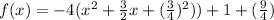
Now rewrite the expression in the form
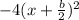`-4(x+(b)/(2))^2`, this is:

`f(x)=-4(x+(3)/(4))^2+(13)/(4)`