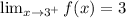Answer:
The limit as x approaches three from the right of f of x is:
3
Explanation:
Based on the graph we observe that the graph of the function increases continuously from x= -∞ to x=3.
There is a open circle at (3,1)
Then at x=3 it takes the value as 7
i.e. when x=3 then f(3)=7
Now after x=3 i.e. to the right of x=3 the graph is a constant line i.e. f(x)=3 for x>3
There is a open circle at (3,3)
Hence, the right hand limit of f(x) at x=3 is: