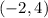Question

Transform the given quadratic function into vertex form f(x) = quadratic function into vertex form f(x) = quadratic function into vertex form
`f(x) = (x-h)^(2) + k` by completing the square.
`a(x-h)^(2) +k` by completing the square.


`f(x) = x^(2) +4x +8`

Answer 1

Vertex form
`f(x) =(x +2)^2 +4`

The vertex is
`(-2,4)`

Explanation:

For a general quadratic function the form is:

`ax ^ 2 + bx + c`

For the function

`f(x) = x ^ 2+ 4x +8`

The values of the coefficients for the function are the following:
`a = 1`,
`b =4`,
`c = 8`

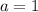Take the value of b and divide it by 2. Then, the result obtained squares it.

`(b)/(2)= (4)/(2)`

`((b)/(2))^2=(2)^2=4`

Add and subtract 4

`f(x) = (x ^ 2 +4x +4) + 8- 4`

Write the expression of the form

`f(x) = (x+(b)/(2))^2 +k`

`f(x) =(x +2)^2 +4`

The vertex is
`(-2,4)`