Answer:
The function intersect the x-axis two times
Explanation:
we have
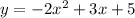
To find the x-intercepts equate the equation to zero
so
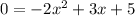
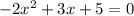
The formula to solve a quadratic equation of the form
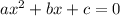 is equal to
is equal to
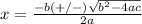
in this problem we have
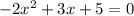
so
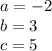
substitute in the formula
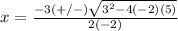
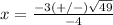
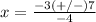
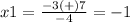
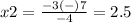
so
The function has two x-intercepts
therefore
The function intersect the x-axis two times