Question

What is the exact value of tan ( 5 pi/8 )

Answer 1

Answer D

Step-by-step explanation:

on edge 2023

Answer 2

Answer: Choice D)
`\tan\left((5\pi)/(8)\right) = - \sqrt{(2+√(2))/(2-√(2))}\\\\\\`

===================================================

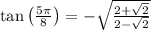
Step-by-step explanation:

Make sure your calculator is in radian mode. Use your calculator to find that tan(5pi/8) = -2.41421 which is approximate.

Since the value is negative, this means the answer is between choices C and D. You can use your calculator to compute those expressions given and you should find it matches with choice D.

----------------------

Further explanation:

We can apply the half angle identity for tangent like so

`\tan\left((x)/(2)\right) = \pm \sqrt{(1-\cos(x))/(1+\cos(x))}\\\\\\\tan\left((5\pi/4)/(2)\right) = -\sqrt{(1-\cos(5\pi/4))/(1+\cos(5\pi/4))}\\\\\\\tan\left((5\pi)/(8)\right) = -\sqrt{(1-\left(-(√(2))/(2)\right))/(1+\left(-(√(2))/(2)\right))}\\\\\\`

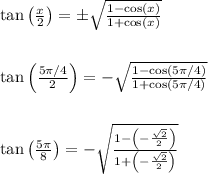
Simplifying further, we get

`\tan\left((5\pi)/(8)\right) = -\sqrt{(1+(√(2))/(2))/(1-(√(2))/(2))}\\\\\\\tan\left((5\pi)/(8)\right) = -\sqrt{(2+√(2))/(2-√(2))}\\\\\\`

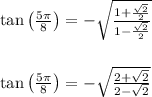
In the last step, I multiplied top and bottom of the outer fraction by 2 to clear out the denominators of the inner fractions.