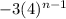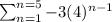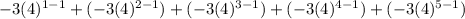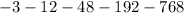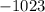Answer:
1) All integers where n ≥ 1
2) -1,023
Explanation:
We are given a G.P. where
First term =
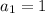
Common ratio = r = 6
nth term of G.P. =
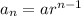
where a is the first term
So, Substitute n = 1
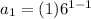
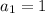
So, Domain for n = All integers where n ≥ 1
Now Find the sum of a finite geometric sequence from n = 1 to n = 5, using the expression