Answer:
3rd Option is correct that is y = - 6.
Explanation:
Given:
Points on the given line: ( -8 , 4 ) and ( 8 , 4 )
To find: Equation of line passing through ( -4 , -6 ) and parallel to given line.
We find the equation of the line using Slope-Point form.
Both line are parallel means Slope of both lines are equal.
Slope of the Required line, m = Slope of given line
=
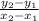
=
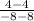
=
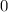
So, the equation of line

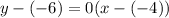
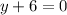
y = - 6
Therefore, 3rd Option is correct that is y = - 6.