Question

Please help! thank you

Answer 1

1. A

2. C

3. D

4. B

5. E

Step-by-step explanation

QUESTION A

The given system of equation is :

`x-4y=-8...(1)`

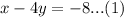
and

`2x-3y=-16...(2)`

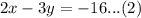
Make x the subject in equation (1)

This implies that;

`x=4y-8...(3)`

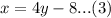
Put equation(3) into equation (2).

`2(4y-8)-3y=-16`

`8y-16-3y=-16`

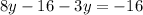
Group like terms;

`8y-3y=-16+16`

`5y=0`

`y=0`

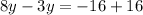
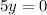
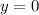
Put y=0 into equation(3).

`x=4(0)-8`

`x=-8`

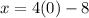
(-8,0)

QUESTION B

First equation:
`x-y=-2`

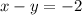
Second equation:
`3x-y=0`

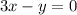
Subtract the first equation from the second equation.

`3x-x-y+y=0+2`

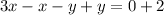
Simplify;

`2x=2`

`x=1`

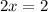
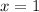
Put x=1 into any of the equations, say the first one.

`1-y=-2`

`-y=-2-1`

`-y=-3`

`y=3`

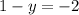
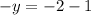
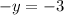
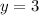
(1,3)

QUESTION C

First equation:
`x+y=-4`

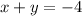
Second equation:
`-3x+2y=2`

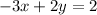
Make y the subject in the first equation;

`y=-x-4`

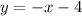
Put y=-x-4 into the second equation;

`-3x+2(-x-4)=2`

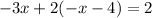
Expand:

`-3x-2x-8=2`

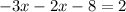
Group like terms:

`-3x-2x=2+8`

`-5x=10`

`x=-2`

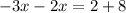
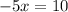
Put x=-2 into
`y=-x-4`

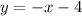
This implies that;

`y=--2-4`

`y=-2`

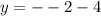
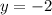
(-2,-2)

QUESTION D

First equation:4x+6y=-12

Second equation: 2x+3y=9

Divide the first equation by 2;

New equation: 2x+3y=-6

Subtract the second equation from the new equation;

`2x-2x+3y-3y=-6-9`

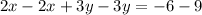
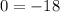`0=-18`. This statement is not true.

The system has no solution;

QUESTION E

First equation:
`x+y=-1`

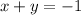
Second equation:
`4x+4y=-4`

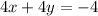
Divide the second equation by 4;

New equation:
`x+y=-1`

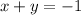
Subtract the second equation from the new equation;

`x-x+y-y=-1+1`

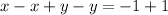
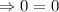`\Rightarrow 0=0` This statement is true.

This system has infinitely many solutions.