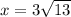Collapse the logarithms into one:
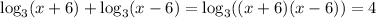
Then write both sides as powers of 3:
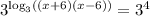
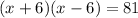
Simplify the left side and solve for
 :
:
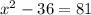
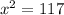

But we're not done yet. Notice that both
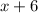 and
and
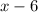 are negative when
are negative when
 . We can't take the logarithm of a negative number (the result isn't real-valued, anyway), so we throw this solution out, and we're left with just
. We can't take the logarithm of a negative number (the result isn't real-valued, anyway), so we throw this solution out, and we're left with just