Question

Measurement The volume in cubic feet of a CD holder can be expressed as V(x) = -x³ - x² + 6x, or, when factored , as the product of its three dimensions. The depth is expressed as 2 - x. Assume that the height is greater than the width. a. Factor the polynomial to find linear expressions for the height and the width. b. Graph the function. Find the x-intercepts. What do they represent? c. What is a realistic domain for the function? d. What is the maximum volume of the CD holder? How can you find the maximum volume of the CD holder?​

Answer 1

a. h = 3 + x; w = x

b. x-intercepts at (-3,0), (0,0), and (2, 0). They represent the values of x for which the volume is zero.

c. 0 ≤ x ≤ 2.

d. 4.061 ft³; Set the derivative of V(x) equal to zero and solve for x.

Explanation:

a. Height and width of the CD holder

V = hwd = -x³ - x² + 6x

Factor out the x = x(6 - x - x²)

Factor the quadratic = x(3 + x)(2 - x)

d = 2 - x

If h > w

h = 3 + x

w = x

b. Graph of V = ƒ(x)

See the first graph below.

The x-intercepts are at (-3,0), (0,0), and (2, 0).

They represent the values of x for which the volume is zero.

c. Realistic domain

We can limit ourselves to the first quadrant, because both the volume and the dimensions must be positive.

The domain is the set of all possible x-values that will make the function work.

Thus, a realistic domain for the function is 0 ≤ x ≤ 2.

d. Find the local maximum

One way to find the local maximum is to set the derivative equal to zero and solve for x to find where the slope of the function is zero.

V(x) = -x³ - x² + 6x

V'(x) = -3x² - 2x + 6 = 0

a = -3, b = -2, c = 6

`x =(-b\pm√(b^2-4ac))/(2a)`

`=(2\pm√((-2)^2-4(-3)*6))/(-6)`

`=(2\pm√((4+ 72)))/(-6)`

`= -(2)/(6)\pm(76 )/(6 )`

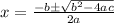
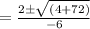
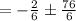
= -⅓ ± (2√19)/6

= -⅓ ± ⅓√19

≈ -0.3333 ± 1.4530

We reject the negative quantity, so

x ≈ 1.1196 ft

V(x) = -(1.1196)³ - (1.1196)² + 6(1.1196)

= -1.4035 - 1.2536 + 6.7178

= 4.061 ft³

The second graph is a blow-up of the first quadrant. It shows that the maximum volume is 4.061 ft³.