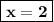Question

Mark the vertex and graph the axis of symmetry of the function.

f(x) = (x – 2)2 – 25

Answer 1

Vertex (2 , -25)

Axis of symmetry: x = 2

Explanation:

Vertex of parabola:

The vertex is the highest point if the parabola open downwards and the lowest point if the parabola opens upward.

f(x) = (x - 2)² - 25

The given quadratic function is in vertex form.

f(x) = a(x - h)² + k

Here, (h , k) is the vertex of the parabola.

h = 2 ; k = -25

`\sf \boxed{\bf Vertex (2 , -25)}`

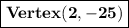
Axis of symmetry:

The axis of symmetry is the vertical line that divides the parabola into two equal halves and it passes through the vertex of the parabola.

Axis of symmetry: x = h

`\sf \boxed{\bf x = 2}`