Question

A well-known author has postulated that 10% of all Medicare claims are fraudulent. Suppose we were to review 10 Medicare claims. The binomial table for this event space is below: B~(10,0.1) P(X=k) P(X≤k) k π k π 0 0.3487 0 0.3487 1 0.3874 1 0.7361 2 0.1937 2 0.9298 3 0.0574 3 0.9872 4 0.0112 4 0.9984 5 0.0015 5 0.9999 6 0.0001 6 1.000 7 0.0000 7 1.000 8 0.0000 8 1.000 9 0.0000 9 1.000 10 0.0000 10 1.000 Given the above information: a. How many claims would we expect to be fraudulent? b. What is the Standard Deviation? c. What is the probability that exactly 3 Medicare claims are fraudulent? d. What is the probability that MORE than 3 claims are fraudulent? e. What is the probability that 3 to 5 claims are fraudulent?

Answer 1

a) 1; b) 0.95; c) 0.0574; d) 0.0128; e) 0.0127

Explanation:

For part a,

To find the number we would expect (the mean), we multiply the sample size by the probability of success:

10(0.1) = 1

For part b,

To find the standard deviation, we use

`√(npq)`

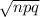
Our n is 10, p is 0.1; this makes q = 1-0.1 = 0.9:

`√(10(0.1)(0.9))=√(0.9)\approx 0.95`

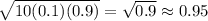
For part c,

We use the binomial table, looking up P(X = 3): 0.0574

For part d,

We start out finding P(X ≤ 3): 0.9872. However, we want P(X > 3), so we subtract from 1:

1-0.9872 = 0.0128

For part d,

We find P(X ≤ 3) and P(X ≤ 5) then subtract:

P(X ≤ 3) = 0.9872; P(X ≤ 5) = 0.9999

0.9999-0.9872 = 0.0127