Question

Line l has the equatin y= 1/3x. Find the equation of the image l after a dilation with a scale factor of 1/2, centered at the origin.

Answer 1

`y = (1)/(3) x + (8)/(3)`

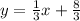
Explanation:

The equation of the line I is
`y = (1)/(3) x`

Scale factor =
`(1)/(2)`, center = (0, 0)

To find the dilated line, we need follow the steps below:

Step 1: Draw the equation of the given line I

Step 2: Let's take a point from the line.

Let's take (2, 6) which is on the line I.

Let's find the dilated point by the scale factor
`(1)/(2)`

Multiply the point (2, 6) by
`(1)/(2)`, we get

(
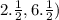`2.(1)/(2) , 6.(1)/(2) )` = (1, 3)

Step 3: Write the equation of the new line (Image I)

The dilated line has the same slope.

So slope (m) =
`(1)/(3)`

x = 1 and y = 3

Now let's find the slope intercept.

y = mx + b

Plug in x = 1, y = 3 and slope (m) =
`(1)/(3)`

3 =
`(1)/(3)`.1 + b

3 =
`(1)/(3)` + b

b = 3 -
`(1)/(3)`

b =
`(3.3 -1)/(3) = (9 -1)/(3) = (8)/(3)`

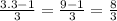
Now let's find the equation of the image I.

y = mx + b

`y = (1)/(3) x + (8)/(3)`

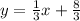
The required equation is
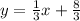`y = (1)/(3) x + (8)/(3)` after the dilation of scale factor.