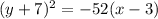Question

The focus of a parabola is (-10, -7), and its directrix is x = 16. Fill in the missing terms and signs in the parabola's equation in standard form. (y )^2= (x )

Answer 1

in order of blanks + 7 - 52 - 3

Explanation:

it is correct i have verified

Answer 2

ANSWER


`(y + 7)^2= - 52(x-3)`

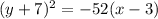
It was given that the parabola has its focus at:

(-10,-7)

and directrix at:

x=16.

We need to determine the vertex of this parabola which is midway between the focus and the directrix.

Therefore the vertex will be at,


`( (16 + - 10)/(2) , - 7)`


`(3, - 7)`

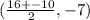
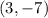
The equation of this parabola is of the form:


`(y-k)^2=4p(x-h)`

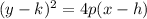
where p is the distance from the vertex to the focus.


`|p| = 16 - 3 = 13`

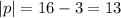
Since the parabola opens towards the negative direction of the x-axis,


`p = - 13`

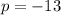
We substitute the vertex and the value for p to get;


`(y - - 7)^2=4( - 13)(x-3)`


`(y + 7)^2= - 52(x-3)`