(a)
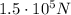
According to the impulse theorem, the impulse exerted on the man during the impact is equal to his change in momentum:
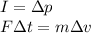
where we have
F = magnitude of the average force
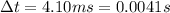 is the contact time
is the contact time
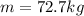 is the mass of the man
is the mass of the man
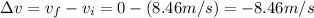 is the change in velocity of the man
is the change in velocity of the man
Solving the formula for F, we find
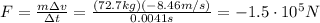
And the negative sign simply means the direction of the force is opposite to the initial velocity of the man (so, the force points upward).
(b) 3705 N
This part of the exercise is exactly identical to part (a), but here the contact time is much longer:
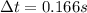
Substituting into the equation, we find
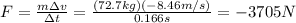
(c) 2992.5 N
We have two forces acting on the man:
- The force that the ground exerts on the man, pointing upward:
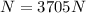
- The force of gravity (weight of the man), pointing downward:
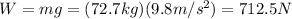
Since the directions are opposite, the resultant force will be
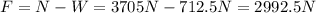
and the direction is upward.