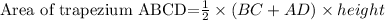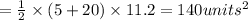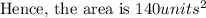Answer:
Explanation:
Given trapezoid ABCD, AB =13, CD = 14, BC = 5 and AD = 20 units.
we have to find the area of trapezoid ABCD
Quadrilateral BEFC is a rectangle, then
EF = BC = 5 units and BE = CF = y units
Let AE = x, then FD = AD - AE - EF = 20 - x - 5 = 15 - x.
By the Pythagorean theorem,
In ΔDFC
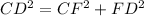
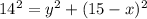 → (1)
→ (1)
In ΔAEB,
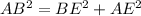
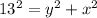 → (2)
→ (2)
Subtract equation 2 from 1
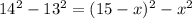
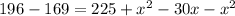
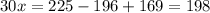
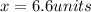
(2) ⇒
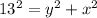
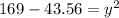

Hence, the height is 11.2 units