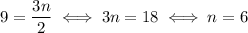Question

How do I do


`\sqrt{9 - n = \sqrt{ (n)/(2) } }`
I need to find the value of n​

Answer 1

I'm assuming that there's a typo and you mean

`√(9-n) = \sqrt{(n)/(2)}`

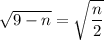
We must use two key facts: the square root is defined only for non-negative inputs, so we must require

`\begin{cases}9-n\geq 0\\(n)/(2)\geq 0\end{cases} \iff \begin{cases}n\leq 9\\n\geq 0\end{cases}`

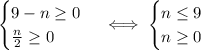
So, we will only accept values in the range

`0 \leq n \leq 9`

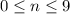
Secondly, where defined, the square root is an injective function. This means that you can only have two equal outputs if you start from two equal inputs:

`√(x)=√(y)\iff x=y`

So, in your case, we have

`√(9-n) = \sqrt{(n)/(2)} \iff 9-n = (n)/(2)`

Adding n to both sides gives

`9 = (3n)/(2) \iff 3n = 18 \iff n = 6`