Answer:
No. Twice as much work will give the ball twice as much kinetic energy. But since KE is proportional to the speed squared, the speed will be
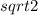 times larger.
times larger.
Step-by-step explanation:
The work done on the ball is equal to the kinetic energy gained by the ball:
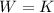
So when the work done doubles, the kinetic energy doubles as well:

However, the kinetic energy is given by
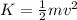
where
m is the mass of the ball
v is its speed
We see that the kinetic energy is proportional to the square of the speed,
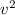 . We can rewrite the last equation as
. We can rewrite the last equation as
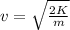
which also means
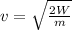
If the work is doubled,

So the new speed is
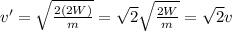
So, the speed is
 times larger.
times larger.